LATTICE DYNAMICS OF CHROMIUM (Cr) AND NIOBIUM (Nb): DFT AND IFCs APPROACH
Keywords:
QE, PW, PBE, MARE, MAE, IFCs, GGA, Ecutwfc, Phonon, Dispersion, Brillouin ZoneAbstract
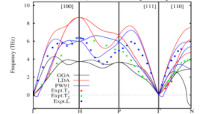
The phonon dispersion curves of Chromium (Cr) and Niobium (Nb) have been calculated from computational approach (first principle using density functional theory) with the exchange correlation functional and analytical (IFCs technique using Born – von Kármán model) with different numbers of interacting nearest-neighbours (NN). The different branches of the phonon band structure follow from the eigen values after diagonalizing the dynamical matrix. The phonon frequencies in the first Brillouin zone were calculated
along the directions of high symmetry,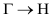 
, 
, 
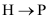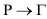and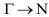 
. Obtain also are the thermodynamic properties from first principle (QUANTUM ESPRESSO) and analytical. It is observed that the phonon dispersion curve of Cr and Nb from IFCs calculation gave a fair agreement with experiment just like the first principle calculations.
Downloads
References
Da Cunha Lima, I. C., Brescansin, L. M and Shukla, M. M. (1974). Lattice Dynamics of Alkali Metals. Physica 72, 179 – 187.
Baroni, S., de Gironcoli, S., Dal Corso, A. and Giannozzi. P. (2001). Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys., 73:515
Born, M. and Huang, K. (1954). Dynamical Theory of Crystal Lattices, Oxford, Clarendon Press, p 420
De Cicco, P. D. and Johnson, F. A. (1969). The quantum theory of lattice dynamics. IV. Proc. R. Soc. London, Ser. A 310, 111
Pick, R., Cohen, M. H. and Martin, R. M. (1970). Microscopic theory of force constants in the adiabatic approximation. Phys. Rev. B 1, 910.
Michel, K. H., Çakır,D., Sevik,C. and Peeters, F. M. (2017). Piezoelectricity in two-dimensional materials: a comparative study between lattice dynamics and ab-initio calculations. Cond-Mat. Mtrl-Sci. 1703.
Phillips, J. C. and Kleinman, L. (1959). New method for calculating wave functions in crystals and molecules. Phys. Rev. 116, 287
Antonick, E. (1959). Approximate formulation of the orthogonalized plane-wave method. J. Phys. Chem. Solids 10, 314
Vosko, S. H., Taylor, R., and Keech, G. H. (1965). Effective Charge Associated with a Displaced Ion in the Orthogonalized-Plane-Wave Formalism. Can. J. Phys. 43, 1187
Animalu, A. O. E. (1966). The total electronic band structure energy for 29 elements. Proc. Roy. Soc. A294, 376
Animalu, A. O. E. and Heine, V. (1965). The screened model potential for 25 elements. Philos. Mag. 12, 1249
Abarenkov, I. V. and Heine, V. (1965). The model potential for positive ions. Phil. Mag. 12, 529-537
Harrison, W. A. (1969). Transition-metal pseudopotentials. Phys. Rev. 181, 1036
Heine, V. and Abarenkov, I. V. (1964). A new method for the electronic structure of metals. Philos. Mag, 9, 465
Animalu, A. O. E. (1974). Electronic structure of transition metals. III. d-band resonance and Regge-pole theory. Phys. Rev. B 10, 4964.
Animalu, A. O. E. (1973). Electronic structure of transition metals. II. Phonon spectra. Phys. Rev. B 8, 3555
Baroni, S., de Gironcoli, S., Dal Corso, A. and Giannozzi. P. (2001). Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys., 73:515
Dal Corso, A. and de Gironcoli, S. (2000). Ab initio phonon dispersions of Fe and Ni. Phys. Rev. B 62, 273
Heid, R., and Bohnen, K. P. (1999). Linear response in a density-functional mixed-basis approach. Phys. Rev. B 60, R3709
Dal Corso, A., Pasquarello, A. and Baldereschi, A. (1997). Density-functional perturbation theory for lattice dynamics with ultra-soft pseudopotentials. Phys. Rev. B 56, R11369
Okocha, Otobo and Alebu Trans. Of NAMP Savrasov, S. Y. and Savrasov, D. Y. (1996). Electron-phonon interactions and related physical properties of metals from linear-response theory. Phys. Rev. B 54, 16487
de Gironcoli, S. (1995). Lattice dynamics of metals from density-functional perturbation theory. Phys. Rev. B 51, 6773
Grabowski, B., Hickel, T. and Neugebauer, J. (2007). Ab initio study of the thermodynamic properties of nonmagnetic elementary fcc metals: Exchange-correlation-related error bars and chemical trends. Phys. Rev. B 76, 024309
Favot, F. and Dal Corso, A. (1999). Phonon dispersions: Performance of the generalized gradient approximation. Phys. Rev. B 60, 11427
Dal Corso, A. (2013). Ab initio phonon dispersions of transition and noble metal: effects of the exchange and correlation functional. J. Phys.: Condensed Matter, 25, 1-9
Margine, E. R., Lambert, H. and Giustino, F. (2016). Electron-Phonon Interaction and Pairing Mechanism in the Superconducting Ca-Intercalated Bilayer Graphene. Scientific Reports, 6, 21414
Al Taleb, A. and Farias, D. (2016). Phonon Dynamics of Graphene on Metals. Journal of Physics: Condensed Matter, 28, 10
Alessandro, E., Jefferson, M. and Bartolomeo C. (2016). Thermal properties of molecular crystals through dispersion-corrected quasi-harmonic ab initio calculations: the case of urea. Chem. Commun. 52, 1820
Press, W. H., Teukolsky, S. A., Vetterling, W. T. and Flannery, B. P. (1989). Numerical Recipes: The Art of Scientific Computing (Cambridge University Press, Cambridge, U.K.).
Gilat, G. and Raubenheimer, L. T. (1966). Accurate numerical method for calculating frequency-distribution functions in solids. Phys. Rev. 144, 390
Giannozzi, P., Baroni, S., Bonini, N., Calandra, M., Car, R., Cavazzoni, C., Ceresoli, D., Chiarotti, G. L., Cococcioni, M., Dabo, I., Dal Corso, A., Fabris, S., Fratesi, G., de Gironcoli, S., Gebauer, R., Gerstmann, U., Gougoussis, C., Kokalj, A., Lazzeri, M., Martin-Samos, L., Marzari, N., Mauri, F., Mazzarello, R., Paolini, S., Pasquarello, A., Paulatto, L., Sbraccia, C., Scandolo, S., Sclauzero, G., Seitsonen, A. P., Smogunov, A., Umari, P. and Wentzcovitch, R. M. (2009). QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys.: Condens. Matter21, 395502.
Giannozzi, P., Andreussi, O., Brumme, T, Bunau, O., Nardelli, M. B., Calandra, M., Car, R., Cavazzoni, C., Ceresoli, D., Cococcioni, M., Colonna, N., Carnimeo, I., Dal Corso, A., de Gironcoli, S., Delugas, P., DiStasio Jr, R. A., Ferretti, A., Floris, A., Fratesi, G., Fugallo, G., Gebauer, R., Gerstmann, U., Giustino, F., Gorni, T., Jia, J., Kawamura, M., Ko, H-Y., Kokalj, A ., Küçükbenli, E., Lazzeri, M., Marsili, M., Marzari, N., Mauri, F.,
Nguyen, N. L., Nguyen, H-V., Otero-de-la-Roza, A., Paulatto, L., Poncé, S., Rocca, D., Sabatini, R., Santra, B., Schlipf, M ., Seitsonen, A. P., Smogunov, A., Timrov, I., Thonhauser, T., Umari, P., Vast, N., Wu, X., and Baroni, S. (2017). Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys.: Condensed. Matter. Vol. 29. 24.
Landau, L. D. and Lifshitz, E. M. (1980). Statistical Physics, 3rd. ed. (Pergamon, London), Pt. 1, Pp. 193
Okocha, Otobo and Alebu Trans. Of NAMP Changyol, L. and Xavier, G. (1995). Ab initio calculation of the thermodynamic properties and atomic temperature factors of SiO2 α-quartz and stishovite. Phys. Rev. B 51, 8610
Bolef, D. I. and De Klerk, J. (1963). Anomalies in the elastic constants and thermal expansion of chromium single crystals. Phys. Rev., 129, 1063
Nakagawa Y. and Woods A. D. B., (1963). Lattice dynamics of niobium. Phys. Rev. Letters 11, 6, 271-274.
