MATHEMATICAL MODELLING ON KIDNAPPING WITH APPREHENDED KIDNAPPERS
DOI:
https://doi.org/10.60787/tnamp-19-29-38Keywords:
Kidnapping, Quick-money, Apprehension, Crime Propagation Number, TerrorismAbstract
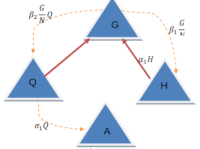
In this work, we develop a mathematical model on kidnapping by incorporating the concept of apprehended kidnappers in a system of ordinary differential equations describing the evolution and propagation of kidnapping as a crime in human society. It accounts for the interaction between kidnappers and vulnerable humans leading to their abduction for the main purpose of ransom payment. We establish the crime propagation number,CPN, in which a CPN<1guarantees a kidnaping free state. The analysis and the numerical simulations of the model suggeststhat, increasing the apprehension rate of kidnappers by Security agents is a better and more effective way of ensuring a kidnapping free society.
Downloads
References
Abati, R. (2009).’ Ransom kidnapping, hostage taking a bewildered Nigeria’. https://www.nigerianvillagesquare.com.
Abraham, U. E.(2010). The social problem of kidnapping and its Implication on the Socio-Economic Development: a case study of Uyo Metropolis. A Master’s Degree Thesis, University of Uyo.
Ezeibe, C. and Eze, M (2012). Political economy of kidnappingin Nigeria–the south east experience. Journal of LiberalStudies Vol.15, No.1.
Tzanelli, R. (2009).“Capitalizing on value: Towards a sociological Understanding of kidnapping”.Sociology, 40(5), pp. 929 – 947.
Caplan,B.(2010).“The strange political economy of kidnaping’’ http://econlog.econlib.org/archieves/2010/06/the_strangepol.html (accessed 1st January, 2022).
Gallagher, R. J (1985). “Kidnapping in the United States and the Development of Federal kidnapping Statute”, B.M. Jenkin(ed.)Terrorism and Personal Protection, pp. 129-45. Boston, MA: Butterworth Publishers.
Okrinya, A. B., and Consul, J. I. (2018). Mathematical Modeling of Kidnapping with Rehabilitation Kidnapping with Rehabilitation Journal of Scientific and Engineering Research, 2018, 5(8):195-205.
Dodo, W. A. (2010). The causes and remedies of kidnapping in Nigeria. The Nigerian Academic Forum, 19(1): 1–4.
Umez, B. N. (2000). Nigeria: real problems, real solutions. Umez: Lagos.
Ugwuoke, C. U. (2011). Nigeria and the menace of kidnapping: Thway forward. The Nigerian Journal of Research and Production Volume, 18(2): 1–14.
Odey, J. O. (2000). The parable of a wasted generation. JO Odey: Ebonyi.
Dennis E. (2020, 14th July). ‘’ Senate passes law prescribing life imprisonment for kidnappers’’. The Guardian: Nigerian Edition.https://guardian.ng/news/senate-passes-law-prescribing-life-
Okrinya, A. B. (2018). Mathematical Model on Kidnapping. Journal of Scientific andEngineering Research.2018, 5(5):
Diekmann., O, Heesterbeek,J. and Johan, M (1990).On the Definition and the Computation of the Basic Reproduction Ratio R_0 in Models for Infectious-Diseases in Heterogeneous Populations.Journal of Mathematical Biology 28(4):365-82.102-110.
Diekmann, O Heesterbrek, J. A. P (2000). Mathematical Epidemiology of infectious diseases.John Wiley and Son.
Driessche, V.D. and Watmough, J. (2002) Reproduction Numbers and Sub- Threshold Endemic Equilibria for Compartmental Models of Disease Transmission.Mathematical Biosciences, 180, 29-48.http://dx.doi.org/10.1016/S0025-5564(02)00108-6.
Allen, J. S. (2007). An introduction to mathematical biology. Pearson Education Inc., Prentice Hall. Upper Saddle River, NJ07458
Onuorah, M. O., and Akinwande,N.I. (2016).Sensitivity Analysis of Lassa Fever Model.European Centre for Research Training and Development UK.www.eajournals.org.14(1).
Okrinya, A. B., and Timinibife, C. N.. (2022). Global Stability Analysis of a Mathematical Model on the Transmission Dynamics Of Covid-19 With Vaccination” International Journal Of Mathematics And Computer Research 10(11) ISSN : 2320-7167.
Published
Issue
Section
License
Copyright (c) 2024 The Transactions of the Nigerian Association of Mathematical Physics

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.




