UNCERTAINTY AND SENSITIVITY ANALYSIS OF THE EFFECTIVE REPRODUCTION NUMBER FOR A DETERMINISTIC MATHEMATICAL MODEL FOR TUBERCULOSIS-SCHISTOSOMIASIS CO-INFECTION DYNAMICS.
DOI:
https://doi.org/10.60787/tnamp.v20.378Keywords:
Tuberculosis, Schistosomiasis, Co-infection, Uncertainty SensitivityAbstract
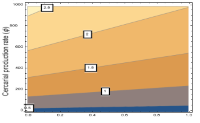
We present the uncertainty and sensitivity analysis of the effective reproduction number for the deterministic mathematical model for tuberculosis-schistosomiasis co-infection dynamics as presented by Ako and Olowu [1]. The results from these contour plots suggest that the effect of the cercarial production, cercarial penetration, the number of schistosome eggs secreted and the successful conversion of the eggs to miracidia, on the hardship of tuberculosis in a populace, is predominantly determined by the medical care levels for individuals with active schistosomiasis. Hence, public health policy should take into account the level of medical care facilities available. With increasing (and sustained) treatment rates for schistosomiasis infections, having a large proportion of active schistosomiasis patients expeditiously receiving medical care will result in a reduction in the disease hardship in the populace.
Downloads
References
Ako, I.I. and Olowu, O.O. (2024), Causes of Backward Bifurcation in a Tuberculosis- Schistosomiasis Co-infection Dynamics. Earthline Journal of Mathematical Sciences 14, Number 4:655–695.
Athithan, S. and Ghosh, M. (2013). Mathematical modelling of TB with the effects of case detection and treatment, Int. J. Dynam. Control 1:223-230, DOI 10.1007/s40435-013-0020-2
Barbour, A.D. (1982). Schistosomiasis. In: R.M. Anderson (Ed.), Population Dynamics of Infectious Diseases, Chapman and Hall, London, pp. 180-208.
Bhunu, C. P., Garira, W. and Magombedze, G. (2009). Mathematical analysis of a two strain HIV/AIDS model with antiretroviral treatment,Acta Biotheoretica, vol. 57, no. 3, pp. 361–381.
Blower, S. M. McLean, A. R., Porco, T. C., Small, P. M., Hopwell, P. C., Sanchez, M. A. and Moss, A.
Cariboni, J., Gatelli, D., Liska, R. and Saltelli, A. (2007). The role of sensitivity analysis in ecological modelling, Ecological modelling 203 (1-2) 167.
Castillo-Chavez, C. and Song, B. (2004). Dynamical Models of Tuberculosis and their Appli- cations, Mathematical Biosciences and Engineering, Volume 1, Number 2, pp. 361-404.
Chen Z., Zou L., Shen D., Zhang W. and Ruan S. (2010). Mathematical modelling and control of schistosomiasis in Hubei Province, China, Acta Tropica 115, 119-125.
Chitnis, N., Hyman, J.M. and Cushing, J.M. (2008). Determining Important Parameters in the Spread of Malaria Through the Sensitivity Analysis of a Mathematical Model, Bulletin of Mathematical Biology 70 (5).
Chiyaka, E. and Garira, W. (2009). Mathematical analysis of the transmission dynamics of schistosomiasis in the human-snail hosts. J Biol Syst; 17:397–423.
Cohen, J.E. (1977). Mathematical models of Schistosomiasis, Ann. Rev. Eco. Syst., 8, pp. 209–233.
Countrymeters (2017). Nigeria Population. https://countrymeters.info/en/Nigeria (accessed on July 19, 2018).
Diaby, M., A. and Iggidr, A. (2016). A mathematical analysis of a model with mating structure.
Proceedings of CARI, 246, pp.402 - 411.
Diaby, M., A., Iggidr, A., Sy, M., and Sene, A. (2014). Global analysis of a schistosomiasis infection model with biological control. Applied Mathematics and Computation, 246, pp.731 - 742.
Feng, Z., Castillo-Chavez, C. and Capurro, A. F. (2000). A Model for Tuberculosis with Exogenous Reinfection, Theoretical Population Biology 57, 235–247
Feng, Z., Curtis, J. and Minchella, D . J. (2001). The influence of drug treatment on the maintenance of Schistosome genetic diversity. J. Math. Bio. 43, 52-68
Feng, Z., Li, C.-C. and Milner, F. A. (2002). Schistosomiasis models with density dependence and age of infection in snail dynamics. Math. Biosci 177-178, 271–286.
Feng, Z., Eppert, A., Milner, F. A. and Minchella, D . J. (2004). Estimation of Parameters Governing the Transmission Dynamics of Schistosomes. Applied Mathematics Letters 17, 1105-1112
Lutambi, A. M., Penny, M. A., Smith, T. and Chitnis, N. (2013). Mathematical modelling of mosquito dispersal in a heterogeneous environment, Mathematical Biosciences 241, 198–216.
Macdonald, G. (1965). The Dynamics of Helminth Infections with Special Reference to Schistosomes. Transaction of the Royal Society of Tropical Medicine and Hygiene. Vol. 59, No. 5, 489-506.
Milner, F. A. and Zhao, R. (2008). A Deterministic Model of Schistosomiasis with Spa- tial Structure. Mathematical Biosciences and Engineering Vol. 5, No. 3, pp. 505–522, http://www.mbejournal.org/
Mushayabasa, S. and Bhunu, C. P. (2011), Modelling Schistosomiasis and HIV/AIDS Cody- namics, Computational and Mathematical Methods in Medicine, Vol. 2011, Article ID 846174, doi:10.1155/2011/846174.
Ngarakana-Gwasira, E. T., Bhunu, C. P., Masocha, M. and Mashonjowa, E. (2016). Transmis- sion dynamics of schistosomiasis in Zimbabwe: A mathematical and GIS Approach, Commun Nonlinear Sci Numer Simulat 35, 137-147.
Okosun K. O. and Smith?, R.(2017). Optimal Control Analysis of Malaria-Scistosomiasis Co- infection Dynamics, Math. Bio. & Eng., Vol. 14, No.2, pp. 377–405. doi:10.3934/mbe.2017024
Okuonghae, D. (2013). A mathematical model of tuberculosis transmission with heterogeneity in disease susceptibility and progression under a treatment regime for infectious cases. Applied Mathematical Modelling 37, 6786–6808
Okuonghae, D. (2014), Lyapunov functions and global properties of some tuberculosis models,
J. Appl. Math. Comput., DOI 10.1007/s12190-014-0811-4.
Okuonghae, D. and Aihie, V. (2008). Case detection and direct observation therapy strategy (DOTS) in Nigeria: Its effect on TB dynamics, Journal of Biological Systems 16(1):1-31.
Okuonghae, D. and Aihie, V. U. (2010). Optimal Control Measures for Tuberculosis Mathemat- ical Models Including Immigration and Isolation Of Infective. Journal of Biological Systems, 18 (01), 17-54. doi:10.1142/s0218339010003160
Okuonghae, D. and Ikhimwin, B. O. (2016). Dynamics of a Mathematical Model for Tuberculo- sis with Variability in Susceptibility and Disease Progressions Due to Difference in Awareness Level. Front. Microbiol. 6:1530. doi: 10.3389/fmicb.2015.01530
Okuonghae, D. and Korobeinikov, A. (2007). Dynamics of Tuberculosis: The effect of Di- rect Observation Therapy Strategy (DOTS) in Nigeria. Mathematical Modelling of Natural Phenomena Vol.2 No.1: Epidemiology pp. 101-113
Okuonghae, D. and Omosigho, S.E. (2011). Analysis of a mathematical model for tuberculosis: What could be done to increase case detection, Journal of Theoretical Biology 269:31–45.
Olowu, O. and Ako, I. (2023). Computational Investigation of the Impact of Availability and Efficacy of Control on the Transmission Dynamics Schistosomiasis, International Journal of Mathematical Trends and Technology Vol. 69 No. 8:1–9.
Olowu, O., Ako, I. I. and Akhaze, R. I. (2021). Theoretical Study of a Two Patch Metapopula- tion Schistosomiasis Model, Transactions of the Nigerian Association Mathematical Physics Vol. 14 (January - March, 2021 Issue):53–68.
Olowu, O., Ako, I. I. and Akhaze, R. I. (2021). On the Analysis of a Two Patch Schistosomiasis Model, Transactions of the Nigerian Association Mathematical Physics Vol. 14 (January - March, 2021 Issue):69–78.
Porco, T.C. and Blower, S.M. (1998). Quantifying the intrisic transmission dynamics of tuberculosis,
Qi, L. and Cui, J. (2013). A Schistosomiasis Model with Mating Structure, Abstract and Applied Analysis, Vol. 2013, Article ID 741386, 9 pages, http://dx.doi.org/10.1155/2013/41386
Qi, L., Xue, M., Cui, J., Wang, Q. and Wang, T. (2018). Schistosomiasis Model and its Control in Anhui Province. Bulletin of Mathematical Biology Volume 2014, 80: 2435–2451, http://doi.org/10.1007/s11538-018-0474-7
UNAIDS-WHO (2004). Epidemiological fact sheet. http://www.unaids.org.
United Nations (2016). Sustainable Development Goals (https:// sustainable develop- ment.un.org/topics/ sustainable development goals, accessed 27 July, 2016).
van den Driessche, P. and Watmough, J. (2002). Reproduction numbers and sub-threshold en- demic equilibria for compartmental models of disease transmission, Mathematical Biosciences 180: 29–48.
Waaler, H., Geser, A. and Andersen, S. (1962). The use of mathematical models in the study of the epidemiology of tuberculosis. Am. J. Public Health Nations Health. 52(6). pp. 1002–1013.
World Health Organization (WHO) (2016). Global tuberculosis report 2016. World Health Organization Press; Geneva, Switzerland.
World Health Organization (WHO) (2023). Global Tuberculosis Report 2023. World Health Organization Press; Geneva, Switzerland.
World Health Organization (WHO) (2023). Schistosomiasis Factsheet 2023. World Health Organization Press; Geneva, Switzerland.
Woolhouse, M.E.J. (1991). On the application of mathematical models of schistosome trans- mission dynamics I: natural transmission, Acta Trop., 49 241.
Zhao, R. and Milner, F. A. (2008). A mathematical model of Schistosoma mansoni in Biom- phalaria glabrata with control strategies, Bulletin of Mathematical Biology, vol. 70, no. 7, pp. 1886–1905.
Downloads
Published
Issue
Section
License
Copyright (c) 2024 The Transactions of the Nigerian Association of Mathematical Physics

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.




