A Study Of Mathematical Modelling Of Control Systems: (A Case Study Of The Inverted Pendulum)
DOI:
https://doi.org/10.60787/tnamp.v21.480Keywords:
Inverted Pendulum, Euler-Lagrange, Ordinary differential equation, Partial differential equation and transfer functionAbstract
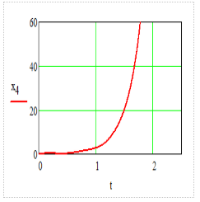
This paper aims to study the mathematical modeling of control systems by examining the dynamics of an inverted pendulum and analyzing the system of nonlinear differential equations associated with it. The objective is to formulate a mathematical model of the inverted pendulum system. The Euler-Lagrange equations were utilized to derive the equations of motion. Additionally, the paper seeks to compute the controllability of the linearized system, obtain the transfer functions, and analyze the state-space representation of the model. Finally, graphical profiles illustrating the system's behavior are provided. This work stabilized the pendulum, enabling precise and rapid control of the carriage's position on the track
Downloads
References
. Chao X. and, Xin Y. (2004), Mathematical modeling of elastic inverted pendulum control system, Journal of Control Theory and Application. 2(3):281-282.
Lal B. P, Barjeev T. and, Hari O. G. (2014), Optimal Control of Nonlinear Inverted Pendulum System Using PID Controller and LQR: Performance Analysis Without and With Disturbance Input. International Journal of Automation and Computing, 11(6):661-670, DOI:1007/s11633-014-0818-1
Sunil K. M. and, Dinesh C. (2014), Stabilization and tracking control of inverted Pendulum using fractional order PID Controller, Journal of Engineering
Krishna M., Faraz A. and Pushpendra K. (2019), Modeling and Analysis of An Inverted Pendulum
Saqib I., Liangyu Z., Safeer U., Adeel M., Muhammad Fasih U. B. (2024) Control strategies for inverted pendulum: A comparative analysis of linear, nonlinear, and artificial intelligence approaches. https://doi.org/10.1371/journal.pone.0298093
Downloads
Published
Issue
Section
License
Copyright (c) 2025 The Transactions of the Nigerian Association of Mathematical Physics

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.




