SOLUTION OF ORDINARY DIFFERENTIAL EQUATION: PERTURBATION ITERATION METHOD APPROACH

Abstract

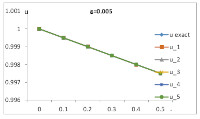
A Perturbation iteration algorithm for solving differential equations of first order is proposed. The applications of the new method to systems of first order ordinary ifferential equations are highlighted with four perturbation parameters considered. The results obtained using the model were compared to the exact solution of a first order ordinary differential equation problem after five iterations were carried out, a minimal error was obtained in the four perturbation parameters considered. Graphical representations of the results clearly show the relationship between the exact solutions and the approximate solutions at each iteration stage.
Based on the results presented, it is concluded that the lower the perturbation parameter, the greater the efficiency of this model. Nevertheless, as the perturbation parameter increases, more iterations is expected to be carried out to get an accurate result. However, the model is efficient in solving first order differential equation.