A DISCRETE TIME EOQ MODEL FOR DELAYED DETERIORATING ITEMS WITH SHORTAGES
Keywords:
Discrete, Deterioration, Lost sale, Backlogged, StockistAbstract
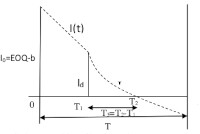
In this work, a discrete time Economic Order Quantity (EOQ) inventory model was developed for delayed deterioration items with shortages. The model consist of three stages in its cycle. In the first stage, the inventory depletes to a certain level due to market
demand only while the second stage depletion occurs due to combined effect of market demand and deterioration. In the final stage, shortage time is assumed by the stockist and are fully backlogged. In the first two stages, the demand rates are different but are
all constants. The model is used to determine the optimal ordering quantity and replenishment cycle. Numerical example is given to illustrate the application of the model and sensitivity analysis carried out to see the effect of parameter changes.
Downloads
References
. Uthayakumar R. and K. V. Geetha, (2009). A Replenishment Policy for Non-instantaneous Deteriorating Inventory System with Partial Backlogging, Tamsui Oxford Journal of Mathematical Sciences, 25, 313-332.
Chang H. J. and Lin W. F. (2010). A partial backlogging inventory model for non-instantaneous deteriorating items with stock-dependent consumption rate under inflation. Yugoslav Journal of Operations Research, 20 (1), 35-54.
Debashis D. and Pavan K. (2015). A partial backlogging inventory model for deteriorating items with time-varying demand and holding cost: An interval number approach Croatian Operational Research Review, CRORR 6, 321- 334.
Yakubu and Sani J. of NAMP Mishra S. S, Gupta S, Yadav S. K, and Rawat S.(2015). Optimization of Fuzzified Economic Order Quantity Model
Allowing Shortage and Deterioration with Full Backlogging. American Journal of Operational Research, 5(5), 103- 110.
Ghare P. M and Shrader G. F.(1963), A Model for Exponential Decaying Inventory, Journal of Industrial Engineering 14 , 238-243.
Covert R.P. and Philip G.C. (1973), An EOQ model for items with Weibull distribution, AHE Trans, 5, 323-326.
Shah, Y.K.(1976), An order level lot size inventory model for Deteriorating item, AIIE Translation, 9(1), 108-112.
Misra, R. B. (1975), Optional production lot size model for a system with deteriorating inventory. International journal of production research, 13, 495-505.
Shah, Y.K. and Jaiswal, M.C., (1977), An order level model for a system with constant rate of deterioration. Opsearch.14, 174-184.
Hollier R. H. and Mark K. L. (1983), Inventory Replenishment polices in a Declining market, International journal of production research 21, 813-826.
Chang H. J. and Dye C.Y (1999), An EOQ Model for Deteriorating Items with Time Varying Demand and Partial Backlogging, Journal of Operational Research Society, 50, 1176-1182.
Wu K.S., Ouyang, L.Y., and Yang, C. T., (2006), An Optimal replenishment policy for non-instantaneous deteriorating items with stock-dependent demand and partial backlogging. International. Journal of Production Economics, 101, 369-384
Musa A. and Sani B. (2009), An EOQ Model for some tropical items that exhibit delay in deterioration. ABACUS, 36(2), 47-52,
Ouyang, L. Y., Wu, K.S., and Yang, C.T, (2006), A study on an inventory model for non-instantaneous deteriorating items with permissible delay in payments. Computers and Industrial Engineering, 51, 637 – 651. Ji, L. (2008), Deterministic EOQ inventory model for non-instantaneous deteriorating items starting with shortage and ending without shortages. IEEE. 1, 1295-1299.
Nahimias, S, (1982), Perishable inventory theory a review, Operational. Research 30, 680-708
Dave U. (1979), On a Discrete-in-Time order-level inventory model for deteriorating items. The journal of the operation research Society, 30(4), 349-354.
Gupta P .N. and Jauhari R. (1993), Optimum ordering interval for constant Decay rate of Inventory Discrete-in- Time. Ganita Sandesh, 7 (1), 12-15.
Aliyu M. D. S. and Boukas E. K. (1998), Discrete-Time Inventory models with deteriorating items, International Journal of Systems Science, 29(9), 1007-1014.
Ferhan M.A., Alex L. and Fahriye U. (2013), Inventory model of deteriorating items on non-periodic discrete-time domains. European Journal of operational Research 230,284-289.
Downloads
Published
Issue
Section
License
Copyright (c) 2024 The Journals of the Nigerian Association of Mathematical Physics

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.




