AREA OF SEMI-CIRCLE FUZZY REGRESSION VIA TRIANGULAR FUZZY NUMBER
DOI:
https://doi.org/10.60787/jnamp-v66-303Keywords:
Inner triangular, Outer triangular, Semi-circleAbstract
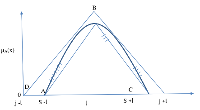
In this paper, we presented a structural, informative and theoretical computation of Area of the Semi-circle fuzzy regression via the triangular fuzzy regression method. The length and the midpoint of the inner triangular and outer triangular fuzzy regression were the required tool applied on the semi-circle fuzzy regression. The resultant regression for the area of semi-circle were obtained for two instances.
Downloads
References
Anand M. C. J and Bharatraj J (2017). Theory of triangular Fuzzy Number, Proceeding of NCATM – 2017 ISB: 978-93-85156-14-7
Ban A. I and Coroianu (2012). Nearest interval, triangular and trapezoidal approximation of a fuzzy number preserving ambiguity, int. J. Approx. Reason 53 page 805-836
Bori P. C, Alejandro R, Jose L. V. and Eduardo RCM (2020). A Fuzzy good programming Approach tofully fuzzy linear regression, IPMU2020, CCIS 1238 page 677 -688. https://doi.org/10.1007/978-3-030-50143-3-53
Diamond P (1988) fuzzy lest square. Information sciences 46, 141-1157
Dongale T. D., Ghatage S. R. and Mudholkar. (2013) Applied philosophy of fuzzy regression. International journal of soft computing and engineering (IJSCE) ISSN: 2231-2307, Vol 2 Issue 6
Garg H. and Kumar K (2020) Novel distance measures for cubic intuitionistic fuzzy set and their applications too pattern recognition and medical diagnosis. Granid compute., page 169-184.
Garg H, and Kumar K (2020), A novel exponential distribution and its based TOPSIS method for interval-valued intuitionist fuzzy set using connection number of SPA theory. Artif.intell Rev., 53, page 595 -624
Jiang H., Kwong C. K., Chan C. Y. and Yung K. L (2019). A multi-objective evolutionary approach for fuzzy regression analysis. Expert system with application 130 page 225-235
Karbasi D, Rabiei M. R and Nazemi A. (2020). A generalied bridge regression in fuzzy environment and its numerical solution by a capable recurrent neutral network. Hindawa Journal of Matematics. Vol. 2020. Article ID: 8838040. http://doi.org/10.1155/2020/8838040
Lee, H. T., and Chen H. C. (2001) Fuzzy regression model with fuzzy input and output data for manpower forecasting. Fuzzy set and system 119, page 205-213
Lee, W, Chen C. and Sui Y. (2010) Application of Half- circle fuzzy number and development of triangular fuzzy numbers control. Selected topics in Applied computer science. Page 335 -340, ISSN 1792-4863
Ren H. and Lio L (2020) A novel distance of intuitionistic trapezoidal number and its-based prospect theory algorithm in multi-atrribute decision making model. Journal of mathematical science and engineering 17(4) page 2905 – 2922 https:www.aimspress.com/journalMBE
Shapiro A. F. and Koissi M. C. (2008). Fuzzy regression and the term structure of interest rate. A least square approach
Tanaka H. Uejima S and Asai K (1982). Linear regression analysis with fuzzy model IEEE Transaction on systems. Man and cybernetic 12(6) page 903 – 907
Tssaur R. C.and Wang H. F. (2009) Necessity analysis of Fuzzy regression equations using goal programming model. International Journal of Fuzzy system. Vol. 11, No. 2 page 107 -115
Wang J. o and Zhang Z (2009) Aggregation operators on intuitionistic trapezoidal fuzzy number and its application to multi-criteria decision making problem, journal syst. Eng. Electron. 20 page 321 -326
Yuan J., and Li C. (2017) A new method for multi-attributed decision making with intuitionistic trapezoidal fuzzy random variable. Int. journal of fuzzy system; 19 page 15-26
Downloads
Published
Issue
Section
License
Copyright (c) 2024 The Journals of the Nigerian Association of Mathematical Physics

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.




