ANALYSIS OF SEMI-CIRCLE FUZZY NUMBER VIA TRIANGULAR APPROACH
DOI:
https://doi.org/10.60787/jnamp-v66-305Keywords:
Semi-circle, Fuzzy analysis, Fuzzy numberAbstract
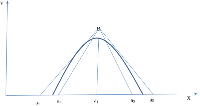
The Semi-circle fuzzy number through the triangular fuzzy number is proposed. The method of obtaining Semi-circle analysis were demonstrated with the use of membership function and introduction of the constant γ. The basic ideas underlying the conventional triangular fuzzy regression were transformed to that of the semi-circle fuzzy analysis.
Downloads
References
Boris P.C, Alejandro R and Jose L. V (2020) A fuzzy goal programming approach to fully linear regression. IPMU, CCIS 1238, page 677 -688. https://doi.org/10.1007/978-3-030-50143-3-53
Chang Y. H., and Ayyub B. M., (1997). Hybrid fuzzy regression analysis and its application. Uncertainty modeling and analysis in civil engineering. Edited by Bilal M. Ayyub, CRC Press Inc.
Dongale T. D., Ghatage S. R. and Mudholkar R. R. (2013) Applied philosophy of fuzzy regression. International journal of soft computing and engineering (IJSCE) ISSN: 2231-2307, Vol 2 Issue 6, page 170 -172
Dubois D. and Prade H. (1978). Operation on fuzzy numbers. International journal of system science. Vol.9, No: 6, page 613 -626
Georgees H. M. and Hidal M.M (2017). Effectiveness of multi-collinearity problem for estimating fuzzy linear regression parameters with application. International journal of science and Nature (IJSN) vol 8, 2 page 284-288
Hojati M, Bector C. R. and Smimou K (2005). A simple method of computation of fuzzy linear regression. European Journal of operational research 166, page 172-184
Jung H. Y, Lee W. J. and Choi S. H. (2019) fuzzy regression model using partition. Journal of physics. Conf. series 1334, 012019. Doi:10.1088/1742-6596/1334/`/012019
Jung H. Y, Lee W. J. and Choi S. H. (2020). Hybrid fuzzy regression analysis using the F transform. MDPI Applied science 10, 6726
Kin H. and Jung H. Y, (2020). Ridge fuzzy regression modelling for solving multicollinearity. MDPI. Mathematic 8, 1572 doi: 10.3390/math809157
Lee W I, Chen C. Y, Chen C. W and Sui Y.C. (2010) Application of half-circle fuzzy number and development of triangular fuzzy number to fuzzy control. Selected topics in applied computer science. ISSN:1792-4863
Ren H. and Luo L. (2020). A novel distance of intuitionistic trapezoidal number and its based prospect theory algorithm in multi-attribute decision making model. Mathematical Biosciences and Engineering, 17(4) page 2905 -2922
Sapiro A.F. and Koissi M.C (2008). Fuzzy regression and the structure of interest Rate: A least square approach
Skrabanek P., Marek J, and Pozdilkova A. (2021). Boscovich fuzzy regression. (MDPI) Mathematics 2021, 9, 685 Basel, Switzerland
Taleshian A. and Rezvani (2016). Multiplication operation of trapezoidal fuzzy number. Journal of physical sciences. Vol 15, age 17 -26
Yang M. S. and Liu H. H. (2003) least square algorithms for interactive fuzzy linear regression model. Fuzzy set and system 135, page 305 – 316
Downloads
Published
Issue
Section
License
Copyright (c) 2024 The Journals of the Nigerian Association of Mathematical Physics

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.




