INFLUENCE OF DAMPING COEFFICIENTS ON THE RESPONSE TO MOVING DISTRIBUTED MASSES OF RAYLEIGH BEAMS RESTING ON BI-PARAMETRIC SUBGRADE
Abstract
This paper is concerned with the dynamic analysis of damping coefficients on the response to moving distributed masses of uniform Rayleigh beams resting on bi-parametric subgrade. In the first instance, The fifth order partial differential equation governing the
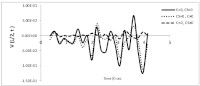
dynamical system is subjected to the finite Fourier sine integral transform to reduce it to a couple second order ordinary differential equation. This resulting coupled ordinary differential equation is then simplifified using the Struble’s Asymptotic techniques to form amenable to Integral transformation techniques. The Closed form Solution thereby obtained is analysed and results in plotted curves revealed that an increase in the value of the damping due to transverse displacement and damping due to strain velocity for a fixed value of shear modulus, foundation stiffness, axial force and rotatory inertia factor decreases the response amplitudes of the beam. However, damping due to resistance to transverse displacement has a more noticeable effects in reducing the response amplitudes of the damped beam than the damping due to strain velocity. It is also found that the critical speed of the moving distributed load which brings about a resonance decreases as the values of damping coefficients increases.
Downloads
References
Fryba, L., (1972): Vibration of solids and structures under moving loads, III edn. Academia, Academy of Sciences of the Czech Republic, Prague.
Struble, R. A. (1962): Nonlinear Differential equations. Mc Graw-Hills, New York, San-Francisco, Toronto, London, Sydney.
Clough, R. and Penzien, J., (2003): Dynamics of structures. Computer & Structures Inc. Third Edition pp. 1-752.
SadikuS. andLeipholz, H.H.E. (1987): On the dynamic of elastic systems with moving concentrated massJs, Ing. Archiv. 57, pp 223-242.
Gbadeyan, J. A. and Oni S.T. (1995): Dynamic behaviours of beams and rectangular plates Under moving loads Journal of sound and vibration. 184, 9-17.
KrylovA.N. (1905): Mathematical collection of papers of the Academy of Science, Vol. 61, Pittsburgh .
Savin, E. (2001): Dynamic Amplification factor and response spectrum for the evaluation of Vibrations of beams under successive moving loads.Journal of sound and vibration Vol. 248(2), pp. 267-288.
Maheshwari, P. and Karuppasamy, K. (2011):Nonlinear response of infinite beams on reinforce Earth beds under moving loads. Geo-Frontiers for American Society of Civil Engineers pp. 4683-4692.
Akinpelu, F.O (2012): The response of Viscously damped Euler-Bernoulli Beam to uniform partially distributed moving loads. Journal of scientific research 3, pp. 199-204.
Alipour A.A. and Zareian F. (2008): Rayleigh damping in structure for uncertainties and treatments. The 14 th World conference on Earthquake Engineering.
Arora, V. (2015): Direct structural damping identification method using complex FRFS. J. Sound vib. 339:304- 323.
Bernal, D. (1994): Viscous Damping inelastic structural response. ASCE Journal of structural Engineering 1994; 120(4): 1240-1254.
Yavari, A., Nouri, M. and Mofid, M. (2002 ). Discrete element analysis of dynamic response of Timoshenko beams under moving mass. Advances in Engineeringsoftwares, 33, pp. 143-153.
Downloads
Published
Issue
Section
License
Copyright (c) 2023 The Journals of the Nigerian Association of Mathematical Physics

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.




