Optimal Assets Allocation For Investors
DOI:
https://doi.org/10.60787/jnamp.v68no1.413Keywords:
Mean, Variance, Return, Risk, Portfolio, Diversification, InvestmentAbstract
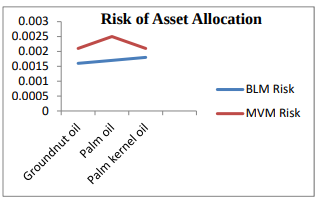
Asset allocation entails allotting investments among many assets. The target of investors is to minimize risk at a given returns or/and maximize returns at a given risk. The aim of this paper is to compare two asset allocations, Black Litterman model (BLM) and Mean Variance Model (MVM). The data used are groundnut oil, palm oil and palm kernel oil. The data is used to estimate values of risk and returns using both asset allocations to compute risk and return of the three assets. It is observed that BLM minimizes risk and maximizes return of its portfolio better than MVM.
Downloads
References
Markowitz, H. (1952). Portfolio selection: Efficient diversification of investment.Cowles foundation, Yale University.
Markowitz, H. (1959). Portfolio selection: Efficient diversification of investment (P, 345) New York, NY: John Wiley and Sons, Inc.
Mobeen, U. R. (2020). Dynamic correlation pattern amongst alternative energy market for diversification opportunity. Journal of Economic Structures, 9(1), 16.
Dimmock, S. G., Wang, N., Yang, J. (2024). The endowment model and modern portfolio theory. Management Science, 70(3), 1554-1579.
Elton, E.J, Gruber, MJ. Brown, S J, and Gootzman, W.N (2010). Modern Portfolio Theory and investment Analysis International. Student Version 8th Edition, John Wiley and Sons Inc, New York.
McGrath, S., Zhao, X., Russell, S., Thombs, B. D.,Benedetti, A. (2020). Estimating the sample mean standard deviation from commonly reported quantiles meta-analysis. Statistical Methods in Medical Research, 5(3), 2520-2537.
Kim, J. H., Lee, Y., Chang W., Fabozzi, F. K. (2021). Mean –variance optimization Asset allocation. The Journal of Portfolio Management, 47(5), 24-40.
Chen, S. D., Lim, A. E., (2020). A Generalized Black Litternman model. Operations Research, 68(2), 381-410.
Ahmad, S. A., Peivandizade, A. (2022).Sustainable portfolio optimization model using promethee ranking: A case study of palm oil buyer companies. Discrete dynamics in Nature and Society, 23(2), 45-52.
Krishnan, A., Williams, L. J., Mcintosh, A. R., Abdi, H. (2011). Partial Least Squares (PLS) methods for neuroimaging: A tutorial and review. Journal of Neuroimage 56(1). 455-475.
Teplova, T., Evgelinia, M., Munir, Q.,Pivnitskaya, N. (2023). Black Litternman model with copula- based views in mean CVaR portfolio optimization framework with weight constraints. Economic Change and Restructuring, 56(1), 515-535.
Maller, R. A., Durand, R. B., Jafarpour, H. (2010). Optimal portfolio choice using the maximum Sharpe ratio. The journal of Risk 12(4). 49-56
Li, Y., Li, J.He, J.,Zhang, S. (2021). The real –time pricing optimization model of smart grid based on the utility function of the logistic function. Journal of Energy, 224(1), 120172.
Tuncer, H. and Xu, F. (2012). The role of log of transformation in forecasting economic variables, Empirical Economics. 42(3), 619-638.
Downloads
Published
Issue
Section
License
Copyright (c) 2024 The Journals of the Nigerian Association of Mathematical Physics

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.




