APPLICATION AND COMPUTATIONAL SIMULATIONS OF NONLINEAR DUFFING OSCILLATOR
DOI:
https://doi.org/10.60787/jnamp.vol69no2.532Keywords:
Duffing oscillator, homotopy perturbation, damped oscillator, nonlinear, vibrationAbstract
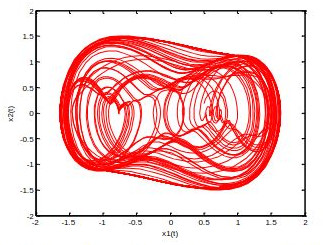
A duffing oscillator occurs due to the motion of a body being subjected to a nonlinear power, linear sticky damping, and periodic forcing. It reveals the oscillations of mechanical systems under the action of a periodic external force. This work studies the application of Duffing oscillators, especially in damping and chaos theory, and also develops an alternative computational method for simulating the Duffing equation. By applying the new homotopy perturbation method and computational method, the findings of this study extract key elements into a model to make it predictive and interpretative. The model is a system with one variable x.x is the inertia or the second time derivative of displacement, are parameters, x is a small damping, The numerical simulation shows the phase plots and system time series.
Downloads
References
Ahmadian, M.T., Mojahedi, M. and Moeenfard, H. (2009). Free vibration analysis of a nonlinear beam using homotopy and modified Lindstedt–Poincare methods, Journal of Solid Mechanics, 1, (2009), 29–36.
Alex, E., (2012). Exact solution With Applications, 59(9), 3222–3228. https://doi.org/10.1016/j.camwa.2010.03.013 of the cubic-quintic Duffing Oscillator. Applied Mathematics Modelling, 37(2013), 2574-2579, https://doi.org/10.1016/jamp.2012.04.005.
Bakhtiari-Nejad, F. and Nazari, M. (2009). Nonlinear vibration analysis of isotropic cantilever plate with viscoelastic laminate. Nonlinear Dynamics, 56, 325–356.
Biazar, J., & Eslami, M. (2011). A new homotopy perturbation method for solving systems of partial differential equations. Computers & Mathematics With Applications, 62(1), 225–234. https://doi.org/10.1016/j.camwa.2011.04.070
Cveticanin, L. (2009). The Approximate Solving Methods for the Cubic Duffing Equation based on the Jacobi Elliptic Functions. International Journal of Nonlinear Sciences and Numerical Simulation, 10(11–12), 1491–1516. https://doi.org/10.1515/ijnsns.2009.10.11-
1491
Durmaz, S., Demirbağ, S. A., & Kaya, M. (2010). High Order He’s Energy Balance Method based on Collocation Method. International Journal of Nonlinear Sciences and Numerical Simulation, 11(Supplement), 1–6. https://doi.org/10.1515/ijnsns.2010.11.s1.1
Ganji, D. D., Gorji, M., Soleimani, S., & Esmaeilpour, M. (2009). Solution of nonlinear cubic-quintic Duffing oscillators using He’s Energy Balance Method. Journal of Zhejiang University. Science A, 10(9), 1263–1268. https://doi.org/10.1631/jzus.a0820651
Ganji, D. D., Alipour, M. M., Fereydoun, A. H., & Rostamian, Y. (2010). Analytic Approach to Investigation of Fluctuation and Frequency of the Oscillators with Odd and Even Nonlinearities. International Journal of Engineering, 23(1), 41–56.
https://www.ije.ir/article_71830_f5343cb56ecaaacaeff10cd79de999f4.pdf
He, J. (2008). Comment on ‘He’s frequency formulation for nonlinear oscillators.’ European Journal of Physics, 29(4), L19–L22. https://doi.org/10.1088/0143-0807/29/4/l02
Khan, Y., Akbarzade, M., & Kargar, A. (2012). Coupling of homotopy and the variational approach for a conservative oscillator with strong odd-nonlinearity. Scientia Iranica, 19(3), 417–422. https://doi.org/10.1016/j.scient.2012.04.004
Kovacic, I. and Brennan M. J. (2011). The Duffing Equation: Nonlinear Oscillators and their Behaviour, John Wiley & Sons, Ltd. Published by John Wiley & Sons, Ltd. ISBN: 978-0- 470-71549-9
Marinca, V., & Herişanu, N. (2006). Periodic solutions of Duffing equation with strong non- linearity. Chaos Solitons & Fractals, 37(1), 144–149. https://doi.org/10.1016/j.chaos.2006.08.033
Meiss, J. (2007). Dynamical systems. Scholarpedia, 2(2), 1629. https://doi.org/10.4249/scholarpedia.1629
Nelson, O. N. E., Yu, Z., Dorian, B. P. and Wang Y. Y. (2018). A new method for the exact solution of Duffing Equation. Journal of Applied Mathematics and Physics, 6, 2718-2726. https://doi.org/10.4236/ jamp 2018.612225.
Suhubi, E. (1988). Nonlinear oscillations, dynamical systems, and bifurcations of vector fields. International Journal of Engineering Science, 26(2), 221–222. https://doi.org/10.1016/0020-7225(88)90107-3
Sunday, J. (2017). The Duffing Oscillator: Applications and Computational simulations. Asian Research Journal of Mathematics, 2(3), 1–13. https://doi.org/10.9734/arjom/2017/31199
Srinil, N., & Zanganeh, H. (2012). Modelling of coupled cross-flow/in-line vortex-induced vibrations using double Duffing and van der Pol oscillators. Ocean Engineering, 53, 83–97. https://doi.org/10.1016/j.oceaneng.2012.06.025
Younesian, D., Askari, H., Saadatnia, Z., & KalamiYazdi, M. (2010). Frequency analysis of strongly nonlinear generalized Duffing oscillators using He’s frequency–amplitude formulation and He’s energy balance method. Computers & Mathematics
Downloads
Published
Issue
Section
License
Copyright (c) 2025 The Journals of the Nigerian Association of Mathematical Physics

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.




