ENTROPY OF METALS BASED ON THE THEORY OF FREE ELECTRON APPROXIMATION USING THERMODYNAMIC POTENTIALS
Keywords:
thermodynamic potential, free electron approximation, strain/deformation, EntropyAbstract
Generalized equation for computing entropy of metals was derived based on theory of free electron approximation using the knowledge of thermodynamic potentials. Poisson ratio representing the negative ratio of transverse and longitudinal strains is
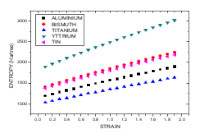
taking into consideration during computation. There is agreement between computed and theoretically obtained experimental value. The experimental results used in this work is theoretically obtained by substituting directly the experimental value of fermi energy (6) into the model used for computation using the mathematical relation between the fermi energy and electron density parameter. Entropy of metals depend on electronic concentration, average electron distance and statistical structure factor. As temperature increases entropy of metals increases due to increase in kinetic energy between interacting electron. Also, increase in entropy as temperature and strain rises is due to atomic disorder and displacement of atoms from their regular atomic site. Entropy of Potassium is the highest during deformation while Tungsten has the lowest entropy during deformation as a result of variation in their atomic
tensile strength.
Downloads
References
Kakani, S. L. and Amit Kakani (2004): Material Science, Publish by New Age International Limited.
Elliott, S.R. (1997): The Physics and Chemistry of Solids. Trinity college, University of Cambridge UK.
Busch, H. and Schade, H. (1976): Lectures on solid state physics. Zurich, Switzerland.
James Patterson and Bernard Bailey, 2010: Solid-State Physics, Introduction to the Theory. Second Edition. Springer, Springer Heidelberg Dordrecht London New York.
Ashcroft N.W. and Mermin D.N. (1976): Solid State Physics. Holt. Rinchart and Winston. New York.
Kittel, C. (1976): Introduction to solid state Physics. Fifth edition. John Wiley and sons. Inc. New York.
Poole, C. P. (2003): Encyclopedic Dictionary of Condensed Matter Physics. Elsevier, Oxford.
Seitz, F. (1940): The Modern Theory of Solids. McGraw-Hill, New York.
Ziman, J. M. (1979): Principles of the Theory of Solids. Cambridge University Press, Cambridge.
Kubo, R and Nagamiya, T. (1969): Solid State Physics. McGraw-Hill, New York.
Altland, A. and Simons, B. (2010): Condensed Matter Field Theory. Cambridge University Press,
Tekuchev, V.V., Kalinkin, D.P. and Ivanova, I.V. (2018): Calculating the Entropy of Solid and Liquid Metals, Based on Acoustic Data. Russian Journal of Physical Chemistry A. Vol. 92, 819-822.
Fang Shao, Zhanqiang Liu and Yi Wana (2008): Thermodynamic Entropy and its Application in Metal Cutting System. Article in Proceedings of SPIE - The International Society for Optical Engineering. China.
Muhammad Naeem, Haiyan He, Fan Zhang, Hailong Huang, Stefanus Harjo, Takuro Kawasaki, Bing Wang, Si Lan, Zhenduo Wu, Feng Wang, Yuan Wu, Zhaoping Lu, Zhongwu Zhang, Chain T. Liu and Xun-Li Wang (2020): Cooperative Deformation in High-Entropy Alloys at Ultralow Temperatures. Science Advances. Vol. 6(13) China.
Adesakin G.E., O. Olubosede, A.T. Fatigun, F.O. Isinkaye, E.A. Oyedele, M.A. Adekoya, O. G. Edema, T.O. Ewumi, F.M. Owolabi, E.O. Aliyu and Agbetuyi Oluranti Adegoke (2020): Extension of Free Electron Theory to the Study of Magnetic Moment of Metals. International Journal of Mechanical and Production Engineering Research and Development (IJMPERD). Vol. 10(3), 9629-9630. India.
Thakor, P. B., Gajjar, P. N., Jani, A. R. (2001). Thermodynamic properties of liquid alkali metals. Condensed Matter Physics, Vol. 4, No. 3(27), 473–480
Baria, J. K. and Jani, A. R. (2010). Enthalpy, Entropy and Helmholtz free energy of transition and rare earth liquid metals. Digest Journal of Nanomaterials and Biostructures. 5 (2), 317 – 322
Michael, W. and Michael, G. (2019). First Principles Calculation of the Entropy of Liquid Aluminum. Entropy. 21
(131).
Downloads
Published
Issue
Section
License
Copyright (c) 2023 The Journals of the Nigerian Association of Mathematical Physics

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.




