CONSTRUCTING BOUND STATES FROM A FINITE POTENTIAL WELL OF VARYING DEPTH
Abstract
Increase in demands of smart devices, due to their current needs in every aspect of human endeavours has opened new opportunities for advances in semiconductor technology. In this study, bound states of a one-dimensional finite square well system, with a varying potential depth were determined, taking the width of the potential to be constant. The allowed energies were determined implicitly as the solutions to the transcendental equations;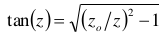 
and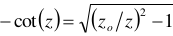 
. Energy eigenvalues are higher for odd solutions than for even solutions. The deeper a potential well is, the higher the energy eigenvalues. At varying depth of a potential well, for each corresponding level of bound states, the deepest well possesses the highest energy. Generally, z0 controls the number of bound states, as z0 grows, for the even solutions, the solutions tend to singularities (2k + 1)π/2 , where k is natural number. For the odd solutions, as z0 grows, solutions tend to singularities that are integer multiples of .
Downloads
References
Melloch, R., J. M. Woodall, E. S. Harmon, N. Otsuka, F. H. Pollak, D. D. Nolte, R.M. Feenstra, and M. A. Lutz (1995), Low-temperature grown III-V materials, Annual Review of Materials Science, 25, 547–600
Akala J. of NAMP Melloch, M. R., D. D. Nolte, J. M. Woodall, J. C. P. Chang, D. B. Janes, and E. S. Harmon (1996), Molecular beam epitaxy of nonstoichiometric semiconductors and multiphase material systems, Critical Reviews in Solid State and Materials Sciences, 21, 189–263.
Pan, J. L. (2001), Optical emission from bound states of semiconductor deep-centers, 9(13), Optics Express, 796– 801
Kolbas, R. M. (1984), Man-made quantum wells: A new perspective on the finite square-well problem, American Journal of Physics, 52, 431–437
Bonfim, O. F. de A. and D. J. Griffiths (2006), Exact and approximate energy spectrum for the finite square well and related potentials, Physics Faculty Publications and Presentation, 8, http://pilotscholars.up.edu/phy_facpubs/8
Palma, G. and U. Raff (2011), A novel application of a Fourier integral representation of bound states in quantum mechanics. American Journal of Physics, 79(2), 201 – 205.
Ahmed, Z. and Bhattacharya, K.(2021), Bound state eigenvalues from transmission coefficients, European Journal of Physics, DOI: 10.1088/1361-6404/ac1149
Ganguly¸ A., S. Kuru, J. Negro, L.M. Nieto (2006), A study of the bound states for square potential wells with position-dependent mass, Physics Letters A 360, 228–233
Bloch, J.-F., and V. Ignatovich (2001), A new approach to bound states in potential wells, American Journal of Physics, 69(11), 1177–1181, doi:10.1119/1.1387043
Abujetas, D. R., Á. Barreda, F. Moreno, J. J. Sáenz, A. Litman, J.-M. Geffrin, and J. A. Sánchez-Gil (2019), Brewster quasi bound states in the continuum in all-dielectric metasurfaces from single magneticdipole resonance meta-atoms, Scientific Reports, 9:16048, https://doi.org/10.1038/s41598-019-52223-4
Gutierrez, T. D. (2014), An introduction to the inverse quantum bound-state problem in one dimension, American Journal of Physics 82, 674, doi: 10.1119/1.4868335, 674 – 680
Hsu, C. W., B. Zhen, A. D. Stone, J. D. Joannopoulos, and M. Soljacˇic (2016), Bound states in the continuum, Nature Reviews (Materials), 1, doi:10.1038/natrevmats.2016.48
Kocher, C. A. (1977), Criteria for bound-state solutions in quantum mechanics, American Journal of Physics, 45(1), 71–74, DOI: 10.1119/1.10913.
Downloads
Published
Issue
Section
License
Copyright (c) 2024 The Journals of the Nigerian Association of Mathematical Physics
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
