Numerical Solution Of Drug Diffusion Model Using The Classic Runge Kutta Method
DOI:
https://doi.org/10.60787/jnamp.v68no1.418Keywords:
Drug diffusion, Fourth-orderRunge-kuttamethod, Ordinary differential Equations, Bio-phase, PharmacokineticsAbstract
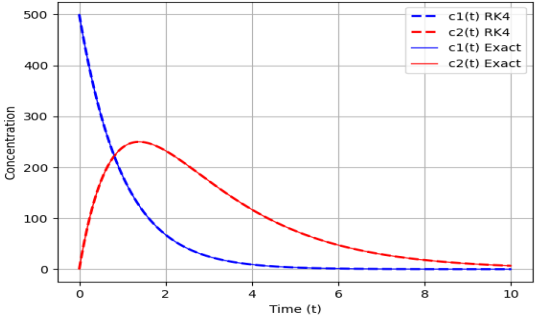
This research investigates the workability approach of the Fourth-order Runge-Kutta method (RK4), to tackle the drug diffusion in the twocompartment model which are the blood and Gastrointestinal tract (GI tract). The theoretical importance of the system of first-order ODEs is considered with initial conditions which served as the drug diffusion into the human body model. The exact solution was calculated using a matrix form of eigenvalues and eigenvectors. The ordinary differential equations describing the problem are solved by the RK4 method on PYTHON. Graphs plots and tables of absolute error analyses are used to show the efficiency of the RK4 method. Our results and finding revealed that RK4 results have approximately the same as exact solution. The analysis of computational error obtained is carried out. At every stage, the numerical result obtained is compared with that of exact solution. The result is also compared with some related result in literature and there is excellent agreement
Downloads
References
Mimi, A.R and Syahirbanun, I. (2022). Fourth-Order Runge-Kutta Method for Solving Applications of System of First-Order Ordinary Differential Equations. Enhanced Knowledge in Sciences and Technology Vol. 2 No. 1, 517-526
Ahmad, N, Charan, S and. Singh, V. P (2015). Study of Numerical Accuracy of Runge-Kutta Second , Third and Fourth-order Method,” International Journal of Computer & Mathematical Sciences vol. 4, no. 6, pp. 111–118,
Chauhan, V and Srivastava, P. K. (2019). Computational techniques based on Rungekutta method of various order and type for solving differential equations,” Int. J. Math. Eng. Manag. Sci., vol. 4, no. 2, pp. 375–386, 2019, doi: 10.33889/ijmems.2019.4.2-030.
Islam, M. A. (2015) “Accurate Solutions of Initial Value Problems for Ordinary Differential Equations with the Fourth-order Runge Kutta Method,” J. Math. Res., vol. 7, no. 3, pp. 41–45, 2015, doi: 10.5539/jmr.v7n3p41.
Kayode, S.J. (2008). An Efficient Zero-Stable Numerical Method for Fourth-Order Differential Equations. International Journal of Mathematics and Mathematical Sciences Volume Article ID 364021, 10 pagesdoi:10.1155/2008/364021
Onkar Warade, N., & Rastogi, P. (2018). Zhou’s Differential Transformation Method for Study of Arm Race Richardson Model. International Kayode, S.J Journal of Mathematics Trends and Technology, 57(6), 382–387. https://doi.org/10.14445/22315373/ijmttv57p552
Roslan, U. A. M. Salleh, Z. and A. Kiliçman, (2013)“Solving Zhou chaotic system using fourth- order Runge- Kutta method,” World Appl. Sci. J., vol. 21, no. 6, pp. 939–944, 2013
Koch-Noble, G. A. (2011)“Drugs in the classroom: Using pharmacokinetics to introduce biomathematical modeling,” Math. Model. Nat. Phenom., vol. 6, no. 6, pp. 227–244, 2011, doi: 10.1051/mmnp/20116612.
Kasim, H, Fudziah I, and Norazak, S. (2016). Solving directly special fourth-order ordinary differential equations using Runge–Kutta type method. Journal of computational and Applied Mathematics vol 306, pp 179-199
Awonuiy, O.D. (2007). Algorithmic collocation approach for direct solution of fourthorder initial- value problems of ordinary differential equations. International Journal of Computational Mathematics, Vol 82, pp 108-120
Downloads
Published
Issue
Section
License
Copyright (c) 2024 The Journals of the Nigerian Association of Mathematical Physics

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.




