MATHEMATICAL INVESTIGATION OF A MASS ACTION EPIDEMIC MODEL
DOI:
https://doi.org/10.60787/tnamp.v23.630Keywords:
Global stability, Lyapunov stability, Mass action, System of ODEs, Invariant regionAbstract
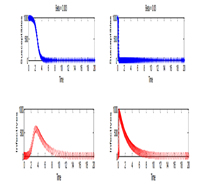
A mass action epidemic model incorporating vital dynamics was developed and examined. This type of model is particularly applicable to several childhood illnesses such as Mumps, Rubella, as well as highly contagious diseases like influenza. We demonstrated that the biologically meaningful region—where solutions are feasible—is positively invariant, meaning that any solution starting within this region remains there for all time. The model features two equilibrium points: the disease-free equilibrium (DFE) and the endemic equilibrium. By utilizing the basic reproduction number, , we established that the DFE is locally asymptotically stable when . Additionally, we proved the global stability of the DFE through an appropriately chosen Lyapunov function. We also found that the endemic equilibrium exists only when . Numerical simulations highlighted the critical role of the contact rate in influencing the transmission dynamics within mass action models.
Downloads
References
Hethcote, H.(2002) : Effects of quarantine in six endemic models for infectious diseases, Math. Biosci., 180,pp. 141–160.
Zhang, J. and Zhien Ma (2003): Global dynamics of an seir epidemic model with saturating contact rate, Mathematical Biosciences.Journal 185 .15-32.
Perelson, A. and Nelson, P.(1991): Mathematical analysis of HIV-1 dynamics in vivo, SIAM Rev. 41 (1999) 3.
Kribs-Zaleta,C and Valesco-Hernandez, J.(2000): A simple vaccination model with multiple endemic states, Math Biosci. 164.183.
Brauer, F. and Van den Driessche,P.(2001): Models for transmission of disease with immigration of infectives, Math. Biosci.171 .143.
Sharomi ,O.(2007): Role of incidence function in vaccine-induced backward bifurcation in some HIV models, Math. Biosci. (2007), doi:10.1016/j.mbs.2007.05.012
Diekmann, O. and Heesterbeek, J.(2000): Mathematical epidemiology of infectious diseases, Wiley series in mathematical and computational biology, John Wiley & Sons, West Sussex, England.
Van den Driessche, P and Watmough, J.(2002): Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math.Biosci. 180, 29–48, doi:10.1016/S0025-5564(02)00108-6
Castillo-Chavez, C. (2002): Approaches for Emerging and Reemerging Infectious Diseases: An Introduction. The IMA Volumes in Mathematics and its Applications. Springer-Verlag, New York,125, pp. 229-250.
Downloads
Published
Issue
Section
License
Copyright (c) 2026 The Transactions of the Nigerian Association of Mathematical Physics

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.