COLLOCATION TECHNIQUE FOR THE NUMERICAL SOLUTION OF THREE DIMENSIONAL VOLTERRA AND FREDHOLM INTEGRAL EQUATIONS BY ORTHOGONAL BASIS FUNCTION
DOI:
https://doi.org/10.60787/jnamp.vol71no.614Keywords:
Collocation technique, Volterra integral equations, Fredholm integral equations, Orthogonal basis function, shifted Legendre polynomiaAbstract
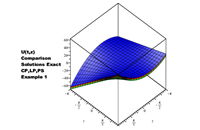
In this paper, standard collocation approximation method is proposed for solving three-dimensional integral equations. New orthogonal polynomials were constructed and used as basis function that gives less rigorous works in terms of computational efforts and enhanced accuracy, Power series and Legendre Polynomials were used as alternative basis functions to checkmate the results of the new Orthogonal Polynomials constructed and used; therefore, three variants of basis functions were used in this work. The proposed methods changed the three-dimensional Volterra and Fredholm integral equations into algebraic system of equations with some unknown constants that were obtained by using MAPLE 18 software. Some numerical examples were solved and less computational works were achieved and the results obtained were in good agreements using three variants with the results available in the literature using different approaches.
Downloads
References
Majeed, S. L. & Omran, H. H. (2008). Numerical methods for solving linear Fredholm-Volterra integral equations. Journal of Al-Nahrain university, 11(3): 131-134.
Dastjerdi, H. L. & Maalek, F. M. (2012). Numerical solution of Volterra-Fredholm integral equations by moving least squares method and Chebyshev polynomials. Appl. Math. Model, 36: 3283-3288.
Zarebnia, M. (2013). A numerical solution of nonlinear Volterra Fredholm integral equations. Journal of applied Analysis and Computation, 3(1): 95-107.
Falade K. I, Muhammad Y. M, Taiwo O. A (2025) Construction and utilization of orthogonal polynomial for the fractional order integro-Volterra-Fredholm differential equations, NIPES Journal of Science and Technology Research 7(1): 46-63.
Alexa, M., Behr, J., Collen-or, D., Fleishman, S., Levin, D & Silva, C. T. (2003). Computing and rendering point set surface Trans. Appl. Comput. Math., 9(1): 3-15.
Levin, D. (1998). The approximation power of moving least squares. Mat Comput, 67(224): 1517- 1531.
Tahereh Eftekhar, Jalil & Khosrow (2018) Numerical solution of three dimensional Volterra-Fredholm Integral equations of the first and second kinds based on Beinstein approximation. Appl. Math. Comput., 10: 299-304. DOI:10,1016/j.anc.2018.07.021.
Dong, C., Chen, Z. & Jang, W. (2013); A muchled homotopy pertubation method for solving the nonlinear mixed Volterra-Fredholm Integral equations. Journal of Computational & Applied Mathematics. 239(1); 359-366.
Wang and Wang (2013) Iterative method and convergence analysis for a kind of mixed nn-linear Volterra-Fredholm Integral equations. Applied Mathematics and Computation., 225: 631-637.
Behzadi Sh.S (2012) Application of Homotopy analysis method for solvimg a class of non-linear Volterra-Fredholm Integro-differential equations. Journal of Applied Analysis & Computation., 2(2):127-136. DOI:10.11948/20/2009.
Shekarabi, F. H., Maleknejad, K. & Khodabin, M. (2014). The petrov-Gerlerkin Method for numerical solution of stochastic Volterra Integral equations. IAENG. Int. Journal. Appl. Math., 44(4):170176
Mohammed, [D.Sh](http://D.Sh). (2016) Shifted Chebyshev Polynomials for solving three dimensional Volterra Integral equations of the second kind. Dol.org/10.48550/arxiv.1609.08539,1-7.
Taiwo, O. A. (1998): On solution of singularly perturbed boundary value problems with a collocation formulation of the Tau-method. Intern. journal of Advances in modeling and simulation., 34 (1,2) France. International Association For Modeling and Simulation.
Taiwo, O. A. & Olagunju, A. S. (2006) Perturbed segmented collocation Tau method for the numerical solution of second order boundary value problems. Journal of the Nigeria Association of Mathematical Physics, 10: 299-304.
Downloads
Published
Issue
Section
License
Copyright (c) 2025 The Journals of the Nigerian Association of Mathematical Physics

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.




