NUMERICAL METHODS FOR STRONGLY CORRELATED ELECTRONS IN ONE DIMENSIONAL FINITE SIX SITES SYSTEM.
DOI:
https://doi.org/10.60787/jnamp-v66-325Keywords:
Numerical exact diagonalization, Hubbard model, electron correlation, Coulomb interaction strength, total energies and eigenstateAbstract
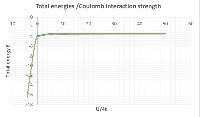
In recent years, the Hubbard model has been subjected to a renewed attention because of its relevance for High-superconductivity, quantum antiferromagnetism, and ferromagnetism thus playing a central role in theoretical investigations of strongly correlated systems. In this paper, we present a numerical exact diagonalization NED of the Hubbard model and a theoretical exact simulation (TES)with the view to obtaining the groundstate-energy spectrum of two electron interaction on a finite six sites lattice system. The extended Hubbard model with nearest and next-nearest neighbour kinetic hopping terms was first applied on the eigenstates available to the two electrons six sites system. The application of the Hubbard model on the various electron eigenstates generated eigenvalue matrix which was solved by numerical exact diagonalization. The results of the ground-state energies from the numerical exact diagonalization were compared with the results obtained from the theoretical exact simulation. The comparison of both methods showed that there is a good correlation between the two results. It is established here that there is a strong correlation between the two electrons at very low negative values of the Coulomb interaction strength .Whereas high values of positive Coulomb interaction strength promotes high kinetic energy between two interacting electrons, since the electrons are now free to hop from one atomic site to another.
Downloads
References
J. Bardeen, L. Cooper and J. Schrieffer, (1957) Theory of Superconductivity. Phys. Rev. B108, 1175
M. Ogata and H. Shiba, (1990) Correlation Functions in One-Dimensional Large-U Hubbard Model: Zero-Field and Finite-Field Cases. Phys. Rev. B 41, 2326
E A Enaibe, E Akpata, N Nenuwe (2016): Analysis of Electron Correlation in the Modified Single Band Hubbard Model. ScienceDomain: Physical Science International Journal, 10(1), p 1-13, Article number PSIJ.24969
H. Rietschel and L. J. Sham, (1983): Superconductivity from non-phonon mechanismsPhys. Rev B28, 5100
D. Pines and P. Nozieres. (1966):The theory of quantum liquids, W. A. Benjamin Inc., New York.
E. H. Lieb and F. Y. Wu, (1968): Ground State Energy of Hubbard Model. Phys. Rev. Lett. 20, 1445
B. S. Shastry, (1986): Exact Integrability of the 1D Hubbard Model. Phys. Rev. Lett. 56, 2453
R. Pariser and R. G. Parr, (1953): A Semi‐Empirical Theory of the Electronic Spectra and Electronic Structure of Complex Unsaturated Molecules. II ,The Journal of Chemical Physics 21, 767.
J. A. Pople, (1953): Electronic interaction in unsaturated hydrocarbonTrnas Faraday Soc., 49, 1375
Y. Zhang and J. Callaway (1989): Extended Hubbard Model in two Dimensions.Phys. Rev. B 39, 9397
T. Ayral, S. Biermann, and P. Werner, (2013): Screening and Non-local Correlations in the Extended Hubbard Model from Self-Consistent Combined GW and Dynamical Mean Field Theory, Phys. Rev. B 87. 125149
C. J. Hamer, (1992): One-and two-hole states in the 2d t-J model via series expansion. Phys. Rev. B 58, 23, 15508
S. Sorella, Y. Otsuka, and S. Yunoki (2012): Absence of a Spin Liquid Phase in the Hubbard Model on the Honeycomb LatticeScientific reports 2, 992.
J. Hubbard, (1963): Electron correlation in Narrow Energy Band. Proc. R. Soc. Lond.A 276, 238
T. Ishino, R. Saito and H. Kamimura, (1990)J. Phys. Soc. Japan, 59, 3886
E A Enaibe, E Akpata, N Nenuwe (2016): Quantitative Evaluation of the Correlation Time and Variational Groundstate Energy of two interacting electrons on (2D) 5 x 5 Square Lattice. North Asian International Research Journal of Science, Engineering and IT, ISSN:2454-7514, Vol. 2(3), p 3-20.
Downloads
Published
Issue
Section
License
Copyright (c) 2024 The Journals of the Nigerian Association of Mathematical Physics

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.




