SPEED OF DIATOMIC MOLECULES IN SHIFTED TIETZ-WEI POTENTIAL
Keywords:
speed of diatomic molecules, eigen energies, SUSYQM, Tietz-Hua potential, Shifted Tietz-Wei potentialAbstract
In this work, the shape invariant formalism of SUSYQM is employed in the derivation of approximate equation of bound state energy eigenvalues of the shifted Tietz-Wei potential (STWP). A Pekeris-type approximation model is used to eliminate the centrifugal term of the Schrödinger equation. The expression of bound state energy eigenvalues is used to obtain equation of speed of the system based on the Hellmann-Feynman theorem. Numerical data of bound state energy eigenvalues and speed of two diatomic molecules including O2 (X 3Σg-) and NO (X2 Πf) are obtained. The calculated energies are in excellent agreement with available literature data of
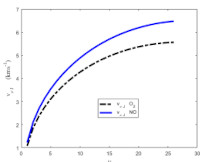
the diatomic molecules. The results also show that the speed of the examined diatomic molecules increases with increase in vibrational quantum number and decreases with increasing rotational quantum number.
Downloads
References
Horchani, R., Al-Kindi, N., and Jelassi, H. (2021). Ro-vibrational energies of caesium molecules with the Tietz-Hua oscillator. Molecular Physics, 119, e1812746. https://doi.org/10.1080/00268976.2020.1812746
Yanar, H., Aydoğdu, O., and Saltı, M. (2016). Modelling of Diatomic Molecules. Molecular Physics, 114, 3134–3142 https://doi.org/10.1080/00268976.2016.1220645
Eyube, E.S., Yerima, J.B., and Ahmed, A.D. (2021). J—State Solutions and Thermodynamic Properties of the Tietz Oscillator. Physica. Scripta. 96, 055001 https://doi.org/10.1088/1402-4896/abe3be
Dong, S.H. (2009). A New Quantization Rule to the Energy Spectra for Modified Hyperbolic-Type Potentials. International journal of quantum chemistry, 109, 701–707. https://doi.org/10.1002/qua.21862
Taskin, F., and Koçak, G. (2010). Approximate solutions of Schrödinger Equation for Eckart Potential with Centrifugal Term. Chinese Physics B, 19, 090314. https://doi.org/10.1088/1674-1056/19/9/090314
Chen, C.Y., You, Y., Lu, F.L., and Dong, S.H. (2013). The Position–Momentum Uncertainty Relations for a Pöschl–Teller Type Potential
and Its Squeezed Phenomena. Physics Letters A, 377, 1070–1075. https://dx.doi.org/10.1016/j.physleta.2013.02.043
Wang, P.Q., Liu, J.Y., Zhang, L.H., Cao, S.Y., and Jia, C.S. (2012). Improved Expressions for the Schiöberg Potential Energy Models for Diatomic Molecules. Journal of Molecular Spectroscopy, 278, 23–26. https://doi.org/10.1016/j.jms.2012.07.001
Hassanabadi, H., Yazarloo, B. H., Mahmoudieh, M., and Zarrinkamar, S. (2013). Dirac Equation Under the Deng-Fan Potential and the Hulthén Potential as a Tensor Interaction via SUSYQM. European Physical Journal Plus, 128, 111. https://doi.org/10.1140/epjp/i2013-13111-4
Eyube, E. S., Ahmed, A. D., and Timtere, P. (2020). Eigensolutions and Expectation Values of Shifted-Rotating Möbius Squared Oscillator. European Physical Journal Plus, 135, 893. https://doi.org/10.1140/epjp/s13360-020-00915-6
Yazarloo, B. H., Hassanabadi, H., and Zarrinkamar, S. (2012). Oscillator Strengths Based on the Möbius Square Potential Under Schrödinger Equation. European Physical Journal Plus, 127, 51. https://doi.org/10.1140/epjp/i2012-12051-9
Qiang, W.C., and Dong, S.H. (2009). The Manning–Rosen Potential Studied by a New Approximate Scheme to the Centrifugal Term. Physica Scripta, 79, 045004. https://doi.org/10.1088/0031-8949/79/04/045004
Mark, Najoji and Eyube J. of NAMP Gu, X.Y., and Dong, S.H. (2011). Energy Spectrum of the Manning-Rosen Potential Including Centrifugal Term Solved by Exact and Proper Quantization Rules. Journal of Mathematical Chemistry, 49, 2053–2062. https://doi.org/10.1007/s10910-011-
-5
Hassanabadi, H., Lu, L. L., Zarrinkamar, S., Liu, G. H., and Rahimov, H. (2012). Approximate Solutions of Schrödinger Equation Under Manning—Rosen Potential in Arbitrary Dimension via SUSYQM. Acta Physica Polonica-Series A General Physics, 122, 650. 10.12693/APhysPolA.122.650
Zhang, L.H., Li, X.P., and Jia, C.S. (2011). Approximate Solutions of the Schrödinger Equation with the Generalized Morse Potential Model Including the Centrifugal Term. International Journal of Quantum Chemistry, 111, 1870–1878. https://doi.org/10.1002/qua.22477
H. Nikoofard, E. Maghsoodi, S. Zarrinkamar, M. Farhadi, H. Hassanabadi (2013). The Nonrelativistic Tietz Potential. Turkish. Journal of Physics. 37, 74 http://doi.10.3906/fiz-1207-1
Kunc, J. A., and Gordillo-Vázquez, F. J. (1997). Rotational−Vibrational Levels of Diatomic Molecules Represented by the Tietz−Hua Rotating Oscillator. Journal of Physical Chemistry A, 101, 1595–1602. https://doi.org/10.1021/jp962817d
Hamzavi, M., Rajabi, A. A., and Thylwe, K.E. (2011). The Rotation-Vibration Spectrum of Diatomic Molecules with the Tietz- Hua Rotating Oscillator. International Journal of Quantum Chemistry, 112, 2701–2705. https://doi.org/10.1002/qua.23285
Hamzavi, M., Rajabi, A. A., and Hassanabadi, H. (2012). The Rotation–Vibration Spectrum of Diatomic Molecules with the Tietz–Hua Rotating Oscillator and Approximation Scheme to the Centrifugal Term. Molecular Physics, 110, 389–393. https://doi.org/10.1080/00268976.2011.648962
Yanar, H., Taş, A., Salti, M., and Aydogdu, O. (2020). Ro-Vibrational Energies of CO Molecule via I proved Generalized Pöschl–Teller Potential and Pekeris-Type Approximation. European Physical Journal Plus, 135, 292. https://doi.org/10.1140/epjp/s13360-020-00297-9
Liu, J.Y., Hu, X.T., and Jia, C.S. (2014). Molecular Energies of the Improved Rosen−Morse Potential Energy Model. Canadian Journal of Chemistry, 92, 40–44. https://doi.org/10.1139/cjc-2013-0396
Tan, M.S., He, S., and Jia, C.S. (2014). Molecular Spinless Energies of the Improved Rosen-Morse Potential Energy Model in D dimensions. European Physical Journal Plus, 129, 264. https://doi.org/10.1140/epjp/i2014-14264-2
Jia, C.S., Zhang, L.H., and Peng, X.L. (2017). Improved Pöschl-Teller Potential Energy Model for Diatomic Molecules. International Journal of Quantum Chemistry, 117, e25383. https://doi.org/10.1002/qua.25383
Liu, H.B., Yi, L.Z., and Jia, C.S. (2018). Solutions of the Klein–Gordon Equation with the Improved Tietz Potential Energy Model. Journal of Mathematical Chemistry, 56, 2982-2994. https://doi.org/10.1007/s10910-018-0927-0
Horchani, R., Jelassi, H., Ikot, A. N., and Okorie, U. S. (2020). Rotation Vibration Spectrum of Potassium Molecules via the Improved Generalized Pöschl‐Teller Oscillator. International Journal of Quantum Chemistry, 121, e26558. https://doi.org/10.1002/qua.26558
Hassanabadi, H., Zarrinkamar, S., and Yazarloo, B. H. (2013). The Nonrelativistic Oscillator Strength of a Hyperbolic-type Potential. Chinese Physics B, 22, 060202. https://doi.org/10.1088/1674-1056/22/6/060202
Hassanabadi, H., Yazarloo, B. H., and Zarrinkamar, S. (2013). Bound-States and the Oscillator Strengths for the Klein-Gordon Equation under Mobius Square Potential. Turkish Journal of Physics, 37, 268-274. doi:10.3906/fiz-1207-21
Khordad, R., and Mirhosseini, B. (2015). Application of Tietz Potential to Study Optical Properties of Spherical Quantum Dots. Pramana Journal of Physics, 85, 723–737. https://doi.org/10.1007/s12043-014-0906-3
Sun, G.H., Dong, S.H., and Saad, N. (2013). Quantum Information Entropies for an Asymmetric Trigonometric Rosen-Morse Potential. Annalen der Physik, 525, 934–943. https://doi.org/10.1002/andp.201300089
Horchani, R., and Jelassi, H. (2020). A Four-parameters Model for Molar Entropy Calculation of Diatomic Molecules via Shifted Tietz-Wei Potential. Chemical Physics Letters, 753, 137583. https://doi.org/10.1016/j.cplett.2020.137583
Gordillo-Vázquez, F. J., and Kunc, J. A. (1998). Statistical–mechanical Calculations of Thermal Properties of Diatomic Gases. Journal of Applied Physics, 84, 4693–4703. https://doi.org/10.1063/1.368712
Yazarloo, B. H., Hassanabadi, H., and Zarrinkamar, S. (2013). Quasi-exact Thermodynamic Properties of a Relativistic Spin- zero System Under Cornell and Generalized Morse Potentials. Turkish Journal of Physics, 37, 394–402. http://doi:org10.3906/fiz-1211-6
Horchani, R., and Jelassi, H. (2020). Effect of Quantum Corrections on Thermodynamic Properties for Dimers. Chemical Physics, 532, 110692. https://doi.org/10.1016/j.chemphys.2020.110692
Falaye, B. J., Ikhdair, S. M., and Hamzavi, M. (2015). Shifted Tietz–Wei Oscillator for Simulating the Atomic Interaction in Diatomic Molecules. Journal of Theoretical and Applied Physics, 9, 151–158. http://doi.org/10.1007/s40094-015-0173-9
Ikot, A. N., Azogor, W., Okorie, U. S., Bazuaye, F. E., Onjeaju, M. C., Onate, C. A., and Chukwuocha, E. O. (2019). Exact and Poisson Summation Thermodynamic Properties for Diatomic Molecules with Shifted Tietz Potential. Indian Journal of Physics, 93, 1171-1179 https://doi.org/10.1007/s12648-019-01375-0
Okorie, U. S., Ibekwe, E. E., Onyeaju, M. C., and Ikot, A. N. (2018). Solutions of the Dirac and Schrödinger Equations with Shifted Tietz-Wei Potential. European Physical Journal Plus, 133, 433. https://doi.org/10.1140/epjp/i2018-12307-4
Roy, A. K. (2014). Ro-vibrational Spectroscopy of Molecules Represented by a Tietz–Hua Oscillator Potential. Journal of Mathematical Chemistry, 52, 1405–1413. https://doi.org/10.1007/s10910-014-0319-z
Downloads
Published
Issue
Section
License
Copyright (c) 2024 The Journals of the Nigerian Association of Mathematical Physics

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.