ON THE PERFORMANCE OF NEW WEIGHTED RIDGE ESTIMATORS FOR MITIGATING HETEROSCEDASTICITY PROBLEM ON A LINEAR REGRESSION MODEL WITH APPLICATION
DOI:
https://doi.org/10.60787/jnamp.vol69no2.531Keywords:
Error variances, Heteroscedasticity, Linear regression model, Monte Carlo simulation, New weighted ridge estimatorsAbstract
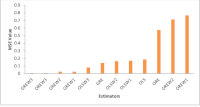
Heteroscedasticity, a common violation of the homoscedasticity assumption in classical linear regression models, adversely affects parameter estimation and predictive accuracy, is a critical issue to be addressed. This study developed and evaluated new weighted ridge estimators for mitigating the effects of heteroscedasticity in linear regression models, particularly where there is little or no multicollinearity. The proposed estimators were derived by combining ridge regression and weighted least squares techniques. Monte Carlo simulations at varying levels of heteroscedasticity, error variances, and sample sizes, were used to assess their performance with the mean square error (MSE) showing that the proposed ORERW estimator performed best when the nature of heteroscedasticity is known, while OREW2 was superior when heteroscedasticity is unknown. Real-life data on passenger car mileage was used to validate the estimators with GREW3 and OREW3 outperforming the traditional methods.
Downloads
References
Ekum, M. I.,Akinmoladun, O. M., Aderele, O. R. and Esan, O. A. (2015). Application of Multivariate Analysis on the effects of World Development Indicators on GDP per capita of Nigeria (1981-2013). International Journal of Science and Technology (IJST), 4(2):254-534.
Johnston, J. (1972). Econometric Methods, 2nd Ed. McGraw-Hill Book Co., Inc., New York.
Gujarati, N. D., Porter, C.D. and Gunasekar, S. (2012)’ Basic Econometrics.’ (Fifth Edition). New Delhi: Tata McGraw-Hill.
Neter, J. and Wasserman, W. (1974) ’Applied Linear Model.’ Richard D. Irwin, Inc.
Fomby, T. B., Hill, R. C. and Johnson, S. R. (1984). ‘Advanced econometric methods.’ Springer- Verlag, New York, Berlin, Heidelberg, London, Paris, Tokyo.
Ayinde, K., Lukman, A. F. and Arowolo, O.T. (2015). Robust regression diagnostics of influential observations in linear regression model. Open Journal of Statistics, 5, 1-11.
Chatterjee, S and Hadi, A. S. (2006). Regression Analysis by Example (Four Edition).
Lukman, A. F., Ayinde, K., Okunola, A. O., Akanbi, O. B. and Onate, C. A. (2018). Classification-Based Ridge Estimation Techniques of Alkhamisi Methods. Journal of Probability and Statistical Sciences. 16 (2), 165-181.
Ayinde, K., Lukman, F., Samuel, O. O. and Ajiboye, S. A. (2018) ‘Some new adjusted ridge estimators of linear regression model’. International Journal of Civil Engineering and Technology, 9 (11), 2838- 2852.
Maddala, G. S. (1988). Introduction to Econometrics, Macmillan, New York.
Lukman, A. F., Ayinde, K. and Ajiboye, S. A. (2017) ‘Monte- Carlo study of some classification-based ridge parameter estimators’. Journal of Modern Applied Statistical Methods, 16 (1), 428-451.
Lukman, A. F., Ayinde, K., Binuomote, S. and Clement, O. A. (2019a). Modified ridge-type estimator to combat multicollinearity: Application to chemical data. Journal of Chemometrics, 33 (5), e3125.
Hoerl, A. E and Kennard, R.W. (1970) ‘Ridge regression: Biased estimation for nonorthogonal problems.’ Technometrics, 12, 55-67.
McDonald, G. C. and Galarneau, D. I. (1975) ‘A Monte Carlo evaluation of some ridge-type estimators’. Journal of the American Statistical Association, 70 (350), 407-412.
Lawless, J. F. and Wang, P. (1976) ‘A simulation study of Ridge and other Regression Estimators’. Communications and Statistics, A5, 307-323.
Wichern, D. and Churchill, G. (1978) ‘A comparison of ridge Estimators’. Technometrics, 20, 301-311.
Gibbons, D. G. (1981) ‘A Simulation Study of Some Ridge Estimators’. Journal of the American Statistical Association, 76 (373), 131-139.
Kibria, B. M. (2003) ‘Performance of Some New Ridge Regression Estimators’. Communications in Statistics- Simulation and Computation, 32 (2), 419-435.
Dorugade, A. V. and Kashid, D. N. (2010). Alternative method for choosing ridge parameter for regression.s International Journal of Applied Mathematical Sciences, 4 (9), 447- 456.
Kibra, B. M. G. and Shipra, B. (2016) ‘Some ridge regression estimators and their performances’. Journal of Modern Applied Statistical Methods, 15 (1), 206- 231.
Lukman, A. F., Ayinde, K., Sek, S. K., and Adewuyi, E. (2019b). A modified new twoparameter in a linear regression model. Modelling and Simulation in Engineering, 2019:6342702. Doi:doi:10.1155/2019/6342702
Aslam, M. and Ahmad, S. (2020). The modified Liu-ridge-type estimator. A new class of biased estimators to address multicollinearity. Communications in Statistics-Simulation and Computation. Doi:10.1080/03610918.2020.1806324.
Zubair, M. A. and Adenomon, M. O. (2021). Comparison of Estimators Efficiency for Linear Regression with Joint Presence of Autocorrelation and Multicollinearity. Science World Journal, Vol. 16 (No.2), 103- 109, ISSN: 1597-6343 (Online), ISSN: 2756-391X (Print).
Hotelling, H. (1933). Analysis of a complex of statistical variables into principal components. Journal of Educational Psychology, 24, 417-441, and 498-520.
Wold, Herman (1985). ‘Partial least square’ In Kotz, Samuel; Johnson, Norman L. (eds.). Encyclopedia of Statistical sciences. 6. New York: Willey. 581-591.
Tabakan, G. (2013) ’Performance of the difference-based estimators in partially linear models.’ Statistics, 47, (2), 329-347.
Hoerl, A. E., Kennard, R. W. and Baldwin, K. F. (1975). ‘Ridge Regression: Some Simulations’. Communications in Statistics,4, 104-123.
Liu, K. (1993) ‘A new class of biased estimate in linear regression.’ Communications in Statistics- Theory and Methods, 22, 393-402, MR1212418.
Khalaf, G. and Shukur, G. (2005). Choosing ridge parameters for regression problems. Communications in Statistics-Theory and Methods, 34, 1177-1182.
Kibra, B. M. G. and Lukman, A. F. (2020). A New Ridge-Type Estimator for the Linear Regression Model: Simulations and Applications. Scientifica. https//doi.org10.1155/2020/9758378.
Aitken, A. C. (1935). ‘On Least Squares and Linear Combination of Observations’. Proceedings of the Royal Statistical Society of Edinburgh, 55, 42-48.
Markov, A. A. (1900). ’Wahrscheinlichkeitsrechnug’. Leipzig; Tuebner.
Cochran, W. G. and Carroll, S. P. (1953) ‘A Sampling Investigation of the Efficiency of Weighting Inversely as the Estimated Variance.’ Biometrics, 9, (4), 447-459.
Park, R. E. (1966). ’Estimation with Heteroscedastic Error Terms’. Econometrica, 34, 888-892.
Hartley, H. O., Rao, J.N.K. and Kiefer, G. (1969) ‘Variance Estimation with One Unit per Stratum’. Journal of the American Statistical Association, 64, 841-851.
Rao, C.R. (1970) ’Estimation of Heteroscedasticity Variances in Linear Models’. Journal of the American Statistical Association 65, 161-172.
Hartley, H. O. and Jayatillake, K. S.E. (1973) ‘Estimation for Linear Models with Unequal Variances’. Journal of the American Statistical Association. 68, 189-192.
Horn, S. D., Horn, R.A. and Duncan, D.B. (1975). ‘Estimating Heteroscedastic Variances in linear model’. Journal of the American Statistical Association, 70, 380-385.
Magnus, J. R. (1978) ’Maximum Likelihood Estimation of the GLS Model with unknown Parameter in the Disturbance Covariance Matrix.’’ Journal of Econometrics, 7, 281-312.
White, H. (1980) ‘A Heteroskedastic-Consistent Covariance Matrix Estimator and A Direct Test for Heteroskedasticity.’ Econometrica , 48 , 817-838.
Cragg, J. G. (1983) ‘More Efficient Estimation in the Presence of Heteroskedasticity of Unknown Form.’ Econometrica, 51, 751-763.
Shin,H. C.(2013) ‘Weighted Least Squares estimation with Sampling Weights.’ Proceedings of the Survey Research Methods Section, the American Statistical Association, 1523-1530.
Balasiddamuni, P., Prakash, K., Rao, K., Prasad, A., Abbaiah, R. and Rayalu, G. (2013) ‘A Minimum Quadratic Unbiased Estimation (MINQUE) of Parameters In A Linear Regression Model With Spherical Disturbances.’ International Journal of Scientific and Technology Research, 2, (5), 135-138.
Shin, H. C. and Kim, J. (2014) ’Weighted Least Squares Estimation with Simultaneous Consideration of Variances and Sampling weights.’ Proceedings of the Survey Research Methods Section, the American Statistical Association, 2972- 2978.
Amalare, A. A., Ayinde, K. and Onanuga, K. (2023). Parameter Estimation of Linear Regression Model with Multicollinearity and Heteroscedasticity Problems. Journal of the Nigerian Association of Mathematical Physics. Vol. 65, 207- 216.
Fuller, W. A. and Rao, J. N. K. (1978) ‘Estimation for a Linear Regression Model with Unknown Diagonal Covariance Matrix’. Annals of Statistics, 6 (5), 1149-1158.
Carroll, R. J. and Ruppert, D. (1988) ‘Transformation and Weighting in Regression’. New York, NY: Chapman & Hall.
Glesjer, H. (1969) ‘A New Test for Heteroscedasticity’. Journal of the American Statistical Association, 64, 316- 323.
Bruesch, T. S. and Pagan, A. R.(1979)‘ A Simple test of heteroscedasticity and random coefficient variation’. Econometrica, 47, 1287 – 1294.
Box, G. E. P. and Hill, W. J.(1974) ‘Correction Inhomogeneity of Variance with Power Transformation Weighting’. Technometrics, 16 (3), 385-389.
Mansson, K., Shukur, G. and Kibra, B. M. G. (2010). On some Ridge Regression Estimators: A Monte Carlo Simulation study under different error variances. Journal of Statistics, 17(1), 1-22.
Idowu, J. I., Oladapo, O. J., Owolabi, A. T. and Ayinde, K. (2022). On the Biased TwoParameter Estimator to Combat Multicollinearity in Linear Regression Model. African Scientific Reports 1:188-204. https://doi.org/10.46481/asr.2022.1.3.57
Seber, F. A. F. (1977). Linear Regression Analysis, John Wiley & Sons, New York, p.64.
Wooldridge, J. M. (2000). Introductory Econometrics: A Modern Approach, South-Western Publishing.
Seber, G. A. and Lee, A. J. (2012). Linear Regression Analysis, Vol. 329: John Wiley & Sons.
Marquardt, D. W. (1970). ’General inverse, Ridge Regression, Biased Linear Estimation and Non-Linear Estimation’. Technometrics, 12, 591-612.
Kleinbaum D. G., Kupper, L. L. and Muller, K. E. (1988) ‘Applied Regression Analysis and Other Multivariate Methods’. Second Edition, PWS-Kent, Boston, Mass, Pp. 210.
Durbin, J. and Watson, G. S. (1951). ‘Testing for Serial Correlation in Least Squares Regression’. Biometrika, Vol. 38, 159- 171
Downloads
Published
Issue
Section
License
Copyright (c) 2025 The Journals of the Nigerian Association of Mathematical Physics

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.